[Java] 비선형 자료구조 - Tree

Tree

• 부모와 자식 노드간의 연결로 구성되어 있으며, 계층 구조가 명확한 그래프의 일종이다.
• 단 하나의 부모 노드 (root)를 가진다.
• 다른 노드와 연결되지 않는 노드는 존재하지 않는다

트리 관련 용어

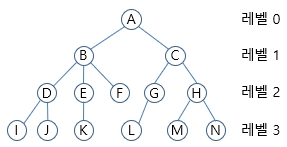
• node : 트리에서 데이터를 저장하는 기본 원소
• branch : 노드와 노드 간의 연결선
• degree : (차수) 노드에 연결된 자식 노드의 수
• level : root로부터 단순 경로의 길이
• height, depth: 최대 레벨 값 + 1

Binary Tree

• 자식 노드가 최대 두개인 노드들로 구성된 트리를 말한다.
• 

Full Binary Tree

• 모든 노드가 0개 혹은 2개의 children을 가지는 이진 트리

Complete Binary Tree

• 마지막 레벨의 노드를 제외한 모든 노드들이 완전하게 채워진 노드
• 해당 구조를 이용해 Binary Heap 자료구조를 만들 수 있다.

Perfect Binary Tree

• 모든 레벨의 노드가 완전하게 채워져 있는 트리

Binary Search Tree

• 정렬된 이진 트리
• 

• 모든 키를 정렬된 순서대로 가져올 수 있다. (전위 순회)

• 검색 방법

  1. 루트에서 시작
  2. 검색 값을 루트와 비교하여, 루트보다 작으면 왼쪽에서 재귀호출을 실시하고 크다면 오른쪽에서 재귀호출을 실시한다.
  3. 일치하는 값을 찾을 때까지 2를 반복한다.
  4. 검색 값이 없으면 null을 반환

Heap

• 일반적으로 binary heap을 구현하여 사용한다.
• 최대/최소값을 빠르게 찾기 위한 자료구조이다.
• 우선순위 큐, Heap sort, Graph 등에 쓰인다.
• Max heap과 Min heap으로 나뉜다.

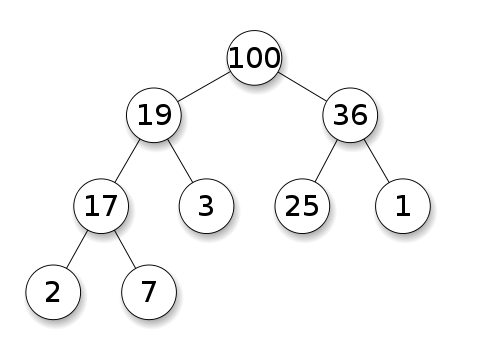
Max Heap

• 가장 큰 값이 루트 노드로 가게 된다.
• 키 값의 대소 관계는 부모 노드와 자식 노드 사이에만 성립하고, 같은 레벨의 노드 위치는 관계없다.
• 재귀적으로 자식 노드의 트리가 모두 Max heap의 조건을 만족한다.

Min Heap

• 가장 작은 값이 루트 노드로 가게 된다.
• 키 값의 대소 관계는 부모 노드와 자식 노드 사이에만 성립하고, 같은 레벨의 노드 위치는 관계없다.
• 재귀적으로 자식 노드의 트리가 모두 Min heap의 조건을 만족한다.

Trie (Retrival tree)

• 트리의 한 종류로, 문자열을 효율적으로 탐색하기 위해 고안된 알고리즘이다.
  • 단어 사전을 찾을 때와 유사한 알고리즘
• 사진은 “A”, “to”, “tea”, “ted” 의 문자열을 저장하는 트라이다.

• 자동완성, 사전 검색 등 문자열을 탐색하는 데에 특화된 자료구조이다.

• 생성 시간 복잡도는 O(MxL), 탐색 시간 복잡도는 O(L)`
  • 제일 긴 문자열의 길이를 L이라 하고, 총 문자열들의 수를 M이라 할 때 시간 복잡도는 위와 같다.

장단점

• 문자열을 탐색할 때, 전부 비교하며 탐색을 하는 것보다 시간 복잡도 측면에서 더 효울적이다.
• 각 노드에서 자식들에 대한 포인터를 모두 저장하고 있어 저장 공간의 크기가 크다는 단점이 있다. (메모리 측면에서 비효율적)

AVL Tree

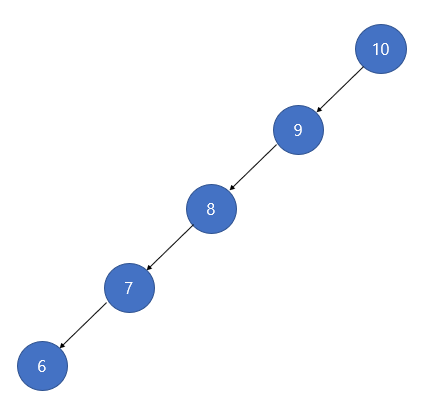
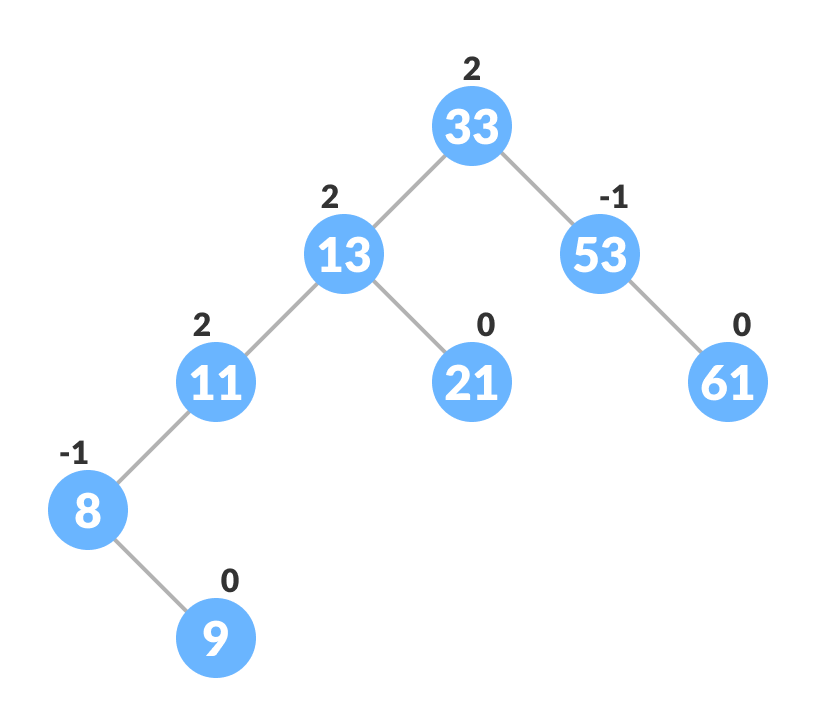
• 한쪽으로 치우친 편향 이진 트리가 되면, 노드 수 대비 트리의 높이가 높아지기 때문에 이를 방지하고자 스스로 균형을 유지하는 이진 트리이다.
• 이진 탐색 트리의 속성을 가진다.
• 왼쪽 서브 트리와 오른쪽 서브 트리의 높이 차이가 최대 1
  • 높이 차이가 1보다 커지면 회전을 통해 균형을 잡아 높이 차이를 줄인다.
• 높이가 $log N$으로 유지되므로 삽입, 검색, 삭제의 시간 복잡도는 $O(logN)$

Operation	Time Complexity
Search	O(log n)
Insertion	O(log n)
Deletion	O(log n)

Balance Factor

• AVL 트리는 균형 판정을 위해 BF를 활용하며, 이는 다음과 같은 공식으로 구할 수 있다.

  $BF(K) = K의 왼쪽 서브트리의 높이 - K의 오른쪽 서브트리의 높이$

Right Rotation

1. y노드의 오른쪽 자식 노드를 z노드로 변경한다.
2. z노드 왼쪽 자식 노드를 y노드의 오른쪽 서브트리(T2)로 변경한다.

Left Rotation

1. y노드의 왼쪽 자식 노드를 z노드로 변경한다.
2. z노드 오른쪽 자식노드를 y노드의 왼쪽 서브트리(T2)로 변경한다.

LL case

• Right Rotation을 사용한다.

LR case

1. BF에 이상이 있는 노드(값이 4인노드)의 왼쪽 자식노드(값이 2인 노드)를 기준으로 Left Rotation
2. BF에 이상이 있는 노드(값이 4인 노드)를 기준으로 Right Rotation

RR case

• Left Rotation을 적용한다.

RL case

1.  BF에 이상이 있는 노드(값이 4인노드)의 오른쪽 자식노드(값이 4인 노드)를 기준으로 Right Rotation
2. 이후 BF에 이상이 있는 노드(값이 4인 노드)를 기준으로 Left Rotation.

Red-Black Tree

• Java의 TreeMap, TreeSet이 Red-black Tree를 베이스로 한 구현을 사용한다.
• AVL tree와 마찬가지로, 편향 이진 트리가 되는 것을 피하기 위한 자가 균형 이진 트리의 한 종류이다.

1. 모든 노드는 빨간색 혹은 검은색이다.
2. 루트 노드는 검은색이다.
3. 빨간색 노드의 자식은 반드시 검은색이다.
4. 모든 리프 노드에서 Black Depth는 같다. (리프 노드에서 루트 노드까지의 경로 중 검은 노드의 개수가 같다.

Recoloring

• $O(logN)$의 시간 복잡도를 가진다.

1. parent 노드를 black의 색으로 교체한다
2. grand parent 노드를 red의 색으로 교체한다.
3. 계속해서 층별 노드의 색을 교체합니다.
4. 이 때, grand parent 노드가 root 노드라면 다시 black으로 교체하여 root 노드를 제외한 모든 노드의 색을 교체한다.

Restructuring

• $O(1)$의 시간 복잡도를 가진다.

1. Double Red가 발생한 자식 노드를 기점으로 parent 노드, grand parent 노드 총 3개의 노드를 정렬한다.
2. 중앙값을 parent 노드로 지정하고, 기존 Tree에 대입한다.
3. parent 노드의 색을 black으로 지정하고, 자식 노드의 색을 red로 지정한다.

B tree

• 하나의 노드에 많은 정보를 가지거나, 두개 이상의 자식을 가질 수도있다.
• B- tree, B* tree, B+ tree 등이 존재한다.